Sprachliche Mitteilungen sind übersichtlich (LWBT)
Aus Philo Wiki
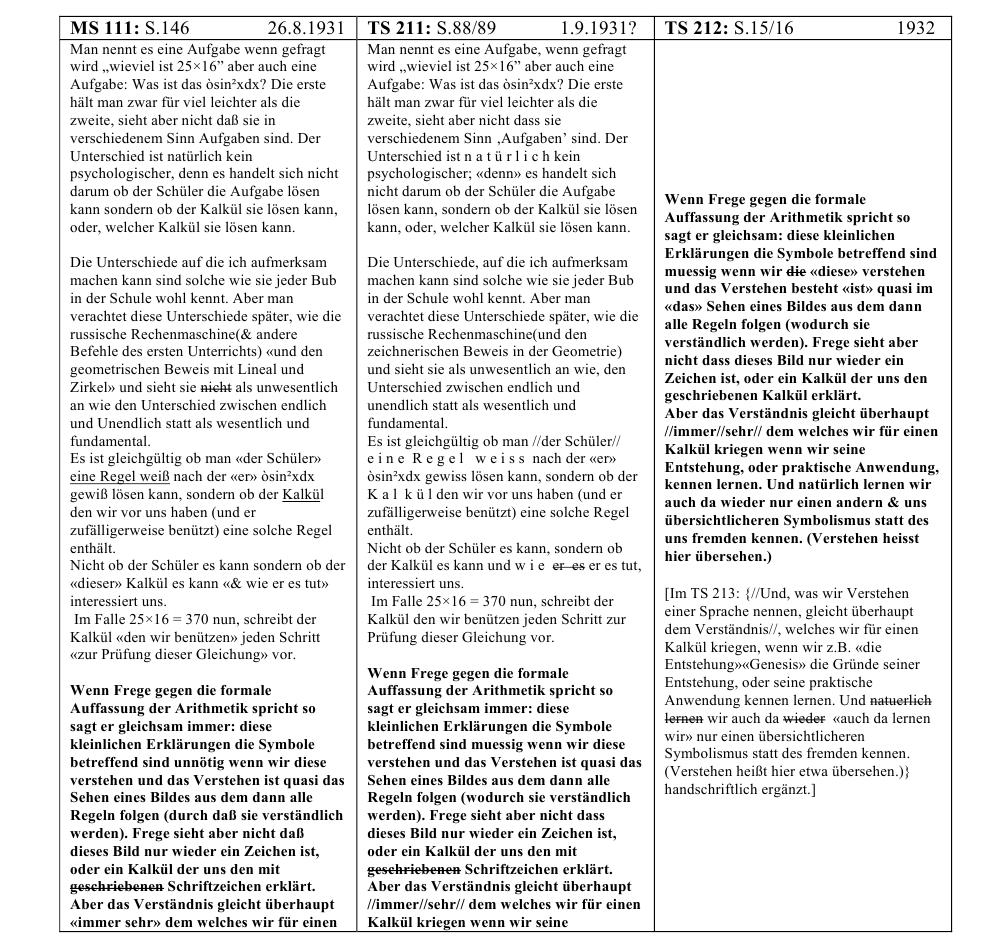
Wenn Frege gegen die formale Auffassung der Arithmetik spricht, so sagt er gleichsam: diese kleinlichen Erklärungen, die Symbole betreffend, sind müßig, wenn wir diese verstehen. Und das Verstehen ist quasi das Sehen eines Bildes, aus dem dann alle Regeln folgen (wodurch sie verständlich werden). Frege sieht aber nicht, daß dieses Bild nur wieder ein Zeichen ist, oder ein Kalkül, der uns den geschriebenen Kalkül erklärt. Aber das Verständnis gleicht überhaupt immer dem, welches wir für einen Kalkül kriegen, wenn wir seine Entstehung, oder seine praktische Anwendung kennen lernen. Und natürlich lernen wir auch da wieder nur einen uns übersichtlichern Symbolismus statt des fremden kennen. (Verstehen heißt hier übersehen.) Wenn komplizierte Vorgänge beim Verstehen des Wortes "und" eine Rolle spielen und das Verstehen etwas für uns Wesentliches ist, wie kommt es, daß diese Vorgänge in der symbolischen Logik nie erwähnt werden? Wie kommt es, daß von ihnen in der Logik nie die Rede ist, noch sein braucht?