Benutzer:PW/Zahlenfolge
<root> <div class='right_side_navigation' style='width:156px;position:fixed;bottom:50px;background-color:#efefef;border-color:#bbbbbb;border-width:1pt;border-style:solid;padding:1px 2px;font-size:8pt;text-align:center;filter:alpha(opacity=90);-moz-opacity: 0.9;opacity: 0.9;'> <comment><!---------------------------------------------------------------------------------------------------------------> </comment> Übersicht<br /> Hauptseite<br /> Letzte Änderungen<br /> Alle Seiten
<hr />
Vo 01. 08.10.10<br /> Bildwelten (CP)<br /> Vo 02. 15.10.10<br /> Vo 03. 22.10.10<br /> Vo 04. 29.10.10<br /> Transkript 2<br /> Vo 05. 05.11.10<br /> Vo 06. 12.11.10<br /> Vo 07. 19.11.10<br /> Vo 08. 03.12.10<br /> Überleitung/D<br /> Vo 09. 10.12.10<br /> Objektorientierung/D<br /> Vo 10. 17.12.10<br /> Vo 11. 14.01.11<br /> Vo 12. 21.01.11<br /> Vo 13. 28.01.11<br />
<hr />
Hilfe<br /> Wiki Hilfe<br /> Infos zur Vorlage<br /> <comment><!---------------------------------------------------------------------------------------------------------------> </comment></div><ignore><includeonly></ignore><ignore></includeonly></ignore></root>
Inhaltsverzeichnis
Kurzzusammenfassung
Auf dieser Seite läuft eine Diskussion rund um die von anna hier gegebene Zahlenfolge "2,4,6,8,10,12,14,16". Sie hat sich in mehrere Richtungen entwickelt, die ich hier kurz zusammenfassen möchte, damit die gesamte Seite leichter lesbar wird. Realgeizt bitte ich die Zusammenfassung zu korrigieren, wenn ich ihr/ihm nicht gerecht geworden bin. --PW 08:21, 19. Dez. 2010 (UTC)
- Für so eine Folge kann es mehrere "Formen dahinter" geben: z.B. eine geschlossene Darstellung oder eine rekursive Darstellung. Diese Darstellungen sind (als Darstellungen) schon dadurch unterschieden, dass man die eine nicht versteht, wenn man eigentlich die andere erwartet.
- Dieses Kriterium der Verschiedenheit (den einen Typ von Darstellung nicht verstehen, wenn man auf den anderen Typ von Darstellung eingestellt ist) versucht PW durch die Tabelle unten plausibel zu machen. Realgeizt stimmt zu, dass die verschiedenen Darstellungen (sogar die sprachliche Darstellung ganz grundsätzlich) zu Missverständnissen führen kann, verortet diesen Hinweis aber auf einer anderen Ebene als seine Ausführungen zur platonischen Form, die das Dargestellte in so einer Darstellung ausmacht.
- Realgeizt wendet ein, dass die Darstellungen f(n) = 2*n + 2 (in der Diskussion auch kurz als: 2n+2) und a_(n+1) = a_n + 2 (in der Diskussion auch kurz als: n+2) nicht auf essentiell verschiedenen Formen verweisen, weil sie beide bloß äquivalente Schreibweisen sind. Die eigentliche Form sei ein abstrakter Zusammenhang (beispielsweise – aber nicht nicht notwendigerweise (!) – die geraden natürlichen Zahlen), die Buchstabenfolge "2,4,6,8,10,12,14,16" verweise auf einige (möglicherweise nicht alle!) Elemente dieses Zusammenhangs und (n+2) oder (2n+2) seien lediglich verschiedene Darstellungsweisen, ein und den selben mathematischen Sachverhalt auf unterschiedliche Weise anzuschreiben. Realgeizt verwendet hier bewusst eine andere Terminologie (siehe zweiter Absatz des Hauptteils unten). Ich bleibe dabei, wie anna im ersten Post (erste Zeile des Hauptteils), die Darstellung (z.B. n+2) und nicht das Dargestellte "Form" zu nennen. --PW 09:43, 20. Dez. 2010 (UTC)
Dann kommt es zu verschiedenen Akzentuierungen und die Diskussion läuft auseinander:
- Realgeizt zeigt eine weitere Möglichkeit auf, "2,4,6,8,10,12,14,16" darzustellen: 2n+2+[n/8]. Diese Darstellung ist anders als n+2 und 2n+2 weil sie ab der neunten Zahl etwas anderes liefert. Er will damit auf eine neben (2n+2) weitere Form hinweisen, die man dem angegebenen Ausschnitt zu Grunde legen kann. Es zeigt sich, dass Zahlenfolgen nicht zuverlässig aus ihren ersten Gliedern rekonstruiert werden können, siehe auch die Wittgensteinzitate unten. Philosophisch führt das weiter in das Problem von Verallgemeinerungen aus endlichen Daten.
- PW interessiert die neunte Zahl nicht, weil es in "2,4,6,8,10,12,14,16" (als endliche Folge interpretiert) nur acht Zahlen gibt. Sein Hauptaugenmerk liegt auf der unterschiedlichen Art, wie 2n+2 und n+2 diese Folge von acht Zahlen erzeugen und wie man dabei vorgehen muss. These: wenn es nur um diese acht Zahlen geht, dann sind sich 2n+2 und 2n+2+[n/8] viel ähnlicher als 2n+2 und n+2. Die Darstellungen 2n+2 und n+2 unterscheiden sich anhand der unterschiedlichen Regeln, nach denen sie auszuwerten sind.
Hauptteil
Hier eine Zeichenkette: 2,4,6,8,10,12,14,16. Gibt es Gemeinsamkeiten? Was fällt Dir auf? ==> "2n+2". Das ist "die Form dahinter".
- Ich habe gerade ohne lang nachzudenken (gewissermaßen instinktiv) die Formel von "n+2" auf "2n+2" umgeschrieben, weil ich gedacht habe, einen Tippfehler gefunden zu haben. "2n+2" wäre eine geschlossene Darstellung der Folge. Aber "n+2" is natürlich genauso eine "Form dahinter", eben eine rekursive Definition dieser Folge. Das zeigt aber, dass der bestimmte Artikel "die" vor "Form dahinter" gewagt ist. --PW 06:38, 3. Dez. 2010 (UTC)
- Ich möchte hier auch noch gern eine Bemerkung anschließen. Ich weiß nicht, ob man bei der rekursiven und der Funktionsdarstellung wirklich von verschiedenen Formen im strengen Sinn sprechen sollte. Vielleicht wäre es besser zu sagen, dass beide Darstellungen auf die selbe Form rekurrieren, aber halt (auf einer anderen Ebene) die Form der Darstellung eine jeweils andere ist. Der Sache nach bleibt es aber die selbe Form – denn würden wir nicht sagen, dass sich die Darstellungen auf das selbe beziehen (was ich als eigentliche Form bezeichnen möchte), hätten sie ja auch nichts Gemeinsames mehr und würden beziehungslos auseinander fallen. Deswegen sollten wir vielleicht die notationelle Darstellung einer Form von der Form selber als dem, worauf sich die Darstellung bezieht, begrifflich trennen. Aber es ließe sich auch eine – nach diesem Sprachgebrauch – wirklich andere Form finden (sogar unendlich viele), sagen wir zum Beispiel die Folge (2n + 2 + floor(n/8)) (floor ist die Abrundungsfunktion): Bei dieser Folge wären die angegebenen Folgenglieder zwar noch gleich, aber das nächste Glied wäre dann 19 (und nicht 18 wie bei 2n+2). Die Bemerkung soll keine bloß mathematische Spitzfindigkeit sein, sondern sie verdeutlicht auch das philosophische Problem, das man sich mit solchen Verallgemeinerungen aufgrund begrenzter Daten einkauft, nämlich dass die allgemeine Form nicht ohne Weiteres aus den Einzelbeispielen rekonstruiert werden kann. Und: Nur weil man ein passendes Erklärungsmuster für eine Reihe von Phänomen gefunden hat, muss dieses Muster nicht zwangsweise das begründende sein. --Realgeizt 01:01, 17. Dez. 2010 (UTC)
- Ich habe mich jetzt gefragt, warum du das, was von 2n+2 bzw. n+2 dargestellt wird, Form nennen möchtest. Natürlich kann man das machen: statt "Dargestelltem" sage ich "Form" und statt "verschiedenen Darstellenden" sehe ich "verschiedene Formen der Darstellung".
- Naja, das ist eine Sprechweise, die sich eben von Platon her anbietet: Die Form entspricht der Idee, und die Darstellung ist ihr (notationelles) Abbild. Ich finde das drängt sich doch aus philosophischer Sicht geradezu auf. --Realgeizt 14:13, 17. Dez. 2010 (UTC)
- Ich habe mich jetzt gefragt, warum du das, was von 2n+2 bzw. n+2 dargestellt wird, Form nennen möchtest. Natürlich kann man das machen: statt "Dargestelltem" sage ich "Form" und statt "verschiedenen Darstellenden" sehe ich "verschiedene Formen der Darstellung".
- Diese neue Terminologie bringt aber nicht neues, wenn von dem Objekt 2,4,6,8,10,12,14,16 die Rede ist. Und da sind die beiden Darstellungen n+2 und 2n+2 so verschieden, wie es nur möglich ist: Angenommen wir geben jemanden auf einer Tafel folgende Zeilen vor, und er soll "Formen dahinter" finden. Diese Formen schreibt er rechts daneben.
| Folge | Form |
| 0 1 2 3 4 | n |
| 0 2 4 6 8 | 2n |
| 0 3 6 9 12 | 3n |
| 0 4 8 12 16 | 4n |
| 0 5 10 15 20 | n+5 |
- Dann werden wir sagen, dass er in der fünften Zeile einen Fehler gemacht hat, weil es vor dem Hintergrund der Struktur der ersten vier Lösungen unverständlich ist, dass in der fünften Zeile auf einmal die Darstellung der Lösung geändert wird. Wir sagen: in der fünften Zeile steht eine falsche Lösung, also eine falsche Form. Wie sollen sich denn Formen desselben Objekts noch mehr unterscheiden als dadurch, dass wenn man eine Form erwartet und die andere serviert bekommt, sie möglicherweise für falsch hält? Dass sie sich nicht dadurch unterscheiden können, dass sie Formen desselben Objekts sind, ist ja klar.
- Mit Verlaub, aber wenn mir jemand sagt, ich soll zu den Folgen auf der linken Seite jeweils die allgemeine Form finden, dann wäre ich aber schwerst empört, wenn mir jemand diese fünfte Zeile für falsch erklärt. Man könnte das allerhöchstens insofern geltend machen, als man einräumt, dass diese Darstellungen etwas schlampig angeschrieben sind, und man bei den ersten 4 Folgen etwas genauer schreiben sollte: f(n) = n, f(n) = 2n, usw., und für die fünfte a_(n+1) = a_n + 5 mit a_0 = 0, wobei n = 0…∞. Aber hier dann noch zu sagen, man hätte die Form falsch erkannt, das fände ich wirklich sehr sehr komisch, und ich würde protestieren: "Du hättest dazusagen müssen, dass auch die Darstellung gleich bleiben muss!" (was in meinen Augen mit der Form gar nichts mehr zu tun hat und eine sehr beliebige und vor allem auch unerwartete Forderung darstellt) Das wäre ja fast wie wenn man in der Schule bei einer Mathematik-Schularbeit 0 Punkte bekommt, weil man die Beispiele auf eine andere Weise gelöst hat, als im Unterricht vorgezeigt wurde. (Dass das tatsächlich von manchem Lehrer nicht so gern gesehen wird hat höchstens didaktische oder Mißtrauensgründe.) -Realgeizt 14:13, 17. Dez. 2010 (UTC)
- Dann werden wir sagen, dass er in der fünften Zeile einen Fehler gemacht hat, weil es vor dem Hintergrund der Struktur der ersten vier Lösungen unverständlich ist, dass in der fünften Zeile auf einmal die Darstellung der Lösung geändert wird. Wir sagen: in der fünften Zeile steht eine falsche Lösung, also eine falsche Form. Wie sollen sich denn Formen desselben Objekts noch mehr unterscheiden als dadurch, dass wenn man eine Form erwartet und die andere serviert bekommt, sie möglicherweise für falsch hält? Dass sie sich nicht dadurch unterscheiden können, dass sie Formen desselben Objekts sind, ist ja klar.
- Wenn du die ersten vier Zeilen wie oben löst und die fünfte nach einem anderen Schema, dann wirst du dir aber die Frage gefallen lassen müssen, warum du auf einmal die Darstellung wechselst und warum du ein Missverständnis riskierst. Und wenn dich jemand missversteht dann bist du "selbst schuld".
- Man kann sich prinzipiell für jede der Folgen, die oben auftreten (und überhaupt für alle solchen Folgen), jeweils ein neues Darstellungssystem ausdenken: die erste notiere ich als klassischen geschlossenen Ausdruck n, die zweite stelle ich rekursiv dar: n+2. Für die dritte verwende ich einen bestimmten Farbverlauf, für die vierte ein akustisches Signal etc. Natürlich kann man den obigen Darstellungen Informationen hinzufügen, damit sie leichter verständlich werden ( z.B.: für 0<=n<=4 sei a_n=n bzw. a_0=0, für alle n sei a_(n+1)=a_n+1) aber natürlich lassen sich auch diese Anweisungen missverstehen. Dass wir sie nicht missverstehen rührt daher, dass wir darauf trainiert sind, solche Formeln auf diese Art und Weise in Zahlenfolgen zu übersetzen. Prinzipiell wäre es aber auch ganz anders möglich.
- Für falsch gehalten wird die fünfte Zeile oben, weil man etwas anderes erwartet. Wenn jemand die ersten vier Zeilen so löst wie oben und dann in die fünfte Zeile einen Farbverauf zeichnet, dann werden wir ihn berechtigterweise fragen, was das soll. Und er wird sich nicht beschweren können mit "Du hättest sagen müssen, dass die Darstellung gleich bleiben muss!". Mein Punkt hier: Missverständnisse sind immer möglich und können nicht grundsätzlich vermieden werden (wie etwa durch genauere Notation), es gibt aber provozierte Missverständnisse und ein solches ist die obige fünfte Zeile oder ein Farbverlauf.
- Worauf ich damit hinaus wollte ist etwas ganz anderes: die Tatsache, dass so ein Missverständnis möglich ist, ist ein Hinweis darauf, dass es sich um verschiedene Formen handelt. Warum? Weil wenn man eine geschlossene Darstellung erwartet und dann den gegebenen Ausdruck n+2 als geschlossene Darstellung interpretiert, dann ist das einfach falsch. Umgekehrt natürlich genau so. --PW 18:17, 17. Dez. 2010 (UTC)
- (Vielleicht vorweg: Ich glaube wir sind uns im Grunde gar nicht so uneinig, aber wir legen das Augenmerk auf ganz unterschiedliche Punkte. Während ich auf die gleichbleibende Form hinter jeder Formel bestehe, machst du auf die zusätzlichen Komplikationen unterschiedlicher Darstellungen aufmerksam. Ich hoffe, diese Charakterisierung trifft einigermaßen den Grund unserer Auseinandersetzung. Und ich bitte um Verständnis, aber mit den nun folgenden Nachbemerkungen will ich es bewenden lassen, weil solche Diskussionen übers Internet sehr schwierig und anstrengend und vor allem auch ganz besonders zeitaufwändig sind. Und man läuft Gefahr, sich zu sehr auf seine Position oder Akzentuierung einzuschießen, und zum Schluss enden wir noch wie der Typ in Duty Calls.)
- In Bezug auf deine obige Ausführung: Ich würde es so sagen: Die Tatsache, dass so ein Mißverständnis möglich ist, ist ein Hinweis darauf, dass es sich um verschiedene notationelle VERMITTLUNGEN ein und derselben Form handelt. Das habe ich oben schon eingeräumt, da sind wir einer Meinung, und gleichzeitig darf es nicht darüber hinwegtäuschen, dass bei jeder Vermittlung nicht nur auf diese oder jene Art vermittelt wird (in der Art einer spezifischen Evaluationsweise, also Regelanwendung), sondern auch ETWAS vermittelt wird. Und dieses etwas ist die Form. Du hast völlig Recht, nicht jede Vermittlung ist gleich, wir sind bestimmte Vermittlungen mehr gewöhnt als andere (z.B. die symbolische Sprache der Mathematik, und innerhalb derer wieder die eine Notation mehr als eine andere (vgl. etwa die verschiedenen Kalküle zur Differentialrechnung nach Newton und Leibniz)); eine Vermittlung über Farbverläufe wäre ungewöhnlich und (daher?) wahrscheinlich auch schwerer zu verstehen. Aber ich bleibe dabei: Das ist ein völlig anderer philosophischer Schauplatz. In meiner ursprünglichen Bemerkung ging es aber um den Rückbezug auf Platon (das ist ja schließlich das Ziel unserer Vorlesung).--Realgeizt 20:56, 18. Dez. 2010 (UTC)
- Insofern würde ich sagen, dass sich die Darstellungen 2n+2 und 2n+2+[n/8] viel ähnlicher sind. Man kann sie nach dem selben Muster evaluieren (bei 1<=n<=7) um dasselbe Objekt "2,4,6,8,10,12,14,16" zu bekommen. Mit n+2 muss man dagegen ganz anders umgehen, damit man "2,4,6,8,10,12,14,16" bekommt. Man muss rekursiv einsetzen.
- Warum für dich 2n+2+[n/8] eine "wirklich andere Form" ist, wird für mich nur dann erklärlich, wenn man annimmt, dass mit "2,4,6,8,10,12,14,16" nicht die ersten 8 geraden natürlichen Zahlen in ihrer natürlichen Ordnung mit Beistrichen dazwischen gemeint sind, sondern: die geraden natürlichen Zahlen schlechthin. Dann unterscheiden sich die Darstellungen 2n+2 und 2n+2+[n/8]. Aber die Voraussetzung für diesen Unterschied ist erst dadurch gegeben, dass (überschwänglich) interpretiert wird, dass mit "2,4,6,8,10,12,14,16" die geraden natürlichen Zahlen gemeint sind und gerade eben nicht die endliche Zeichenkette. Und diese Interpretation führt dann auch zu der philosophischen Schwierigkeit der Verallgemeinerungen und der Tatsache, dass Mathematiker bei Intelligenztests, wenn es um "die richtige" Fortsetzung von Zahlenfolgen geht, furchtbar schlecht sind, weil ihnen sofort überabzählbar viele sinnvolle Fortsetzungen einfallen (für n gegebene Zahlen setze ein Polynom vom Grad n+1 an).
- Was, wieso denn? Meine unterschiedlichen Formen ergeben sich genau aus der Beobachtung, dass mit "2,4,6,8,10,12,14,16" eben noch nicht notwendigerweise die geraden natürlichen Zahlen gemeint sind! Deswegen gebe ich ja auch illustrativ eine Folge an, die 19 als nächstes Glied produziert. (Im Gegensatz dazu beziehen sich sowoh (2n+2) als auch die rekursive Folge (n+2) auf die geraden natürlichen Zahlen: Damit scheint also – zwar nicht notwendigerweise, aber eben dem Schein nach – mehr vorausgesetzt zu sein.) Und es ist natürlich richtig, dass deine 2 Angaben jeweils anders zu evaluieren sind, aber das halte ich ehrlich gesagt im platonischen Kontext für eher nebensächlich. Es soll damit selbstverständlich nicht gesagt sein, dass die 2 Darstellungen identisch sind, natürlich sind sie das nicht! Aber sie sind äquivalent und sie sind vom selben Status. Sie sind aber von einem anderen Status als die Form auf die sie sich beziehen. In einer Analogie könnte man sagen: Sie verhalten sich zur beiden gemeinsamen Form (nach meiner Sprechweise) wie das mit Akzidentellem behaftete Einzelding (also Abbild) zum Urbild. --Realgeizt 14:13, 17. Dez. 2010 (UTC)
- Warum für dich 2n+2+[n/8] eine "wirklich andere Form" ist, wird für mich nur dann erklärlich, wenn man annimmt, dass mit "2,4,6,8,10,12,14,16" nicht die ersten 8 geraden natürlichen Zahlen in ihrer natürlichen Ordnung mit Beistrichen dazwischen gemeint sind, sondern: die geraden natürlichen Zahlen schlechthin. Dann unterscheiden sich die Darstellungen 2n+2 und 2n+2+[n/8]. Aber die Voraussetzung für diesen Unterschied ist erst dadurch gegeben, dass (überschwänglich) interpretiert wird, dass mit "2,4,6,8,10,12,14,16" die geraden natürlichen Zahlen gemeint sind und gerade eben nicht die endliche Zeichenkette. Und diese Interpretation führt dann auch zu der philosophischen Schwierigkeit der Verallgemeinerungen und der Tatsache, dass Mathematiker bei Intelligenztests, wenn es um "die richtige" Fortsetzung von Zahlenfolgen geht, furchtbar schlecht sind, weil ihnen sofort überabzählbar viele sinnvolle Fortsetzungen einfallen (für n gegebene Zahlen setze ein Polynom vom Grad n+1 an).
- wenn ich nur die Zahlen "2,4,6,8,10,12,14,16" kenne oder mich in beliebigen Formelevaluationen nur auf die ersten 8 Terme beschränke, dann liefern (2n+2) und 2n+2+[n/8] genau dasselbe. Der 19er ist mir dabei egal. Für die Erzeugung dieser Zeichenkette aus 8 Zahlen ist es vollkommen irrelevant was passiert, wenn man in die Formel n=8 einsetzt.
- Entscheidender ist der Unterschied zwischen (2n+2) und n+2, weil das n in beiden Ausdrücken verschiedene Funktionen hat. Es ist eine andere Handlung die Zahlen 0,1,2,3,4,5,6,7 in (2n+2) einzusetzen, als schrittweise mit 2 startend immer die zuletzt gewonnene Zahl in n+2 einzusetzen. Man muss einfach andere Spielregeln befolgen, um mit beiden Formeln auf das Ergebnis "2,4,6,8,10,12,14,16" zu kommen. Inwiefern das im platonischen Kontext nebensächlich oder nicht nebensächlich ist, kann ich nicht entscheiden. Bei Wittgenstein ist Regelfolgen aber ein großes Thema.
- Ich will nicht bestreiten, dass 2n+2+[n/8] eine andere Form ist als 2n+2 oder n+2. Ich meine aber, dass der Unterschied zwischen 2n+2 und n+2 deutlich größer (nämlich im obigen Sinn) ist als zwischen 2n+2+[n/8] und 2n+2. --PW 18:17, 17. Dez. 2010 (UTC)
- Das ist ein hilfreicher und interessanter Hinweis, dass die Zahlenfolge nur aus diesen Gliedern und keinen weiteren bestehen könnte. Unter dieser von dir gesetzten Eingrenzung sind die beiden von mir angegebenen Forme(l)n äquivalent – das ist aber natürlich nicht der Definitions- und Bildbereich, den ich vor Augen hatte. Der Hinweis verdeutlicht damit allerdings nur meine Bemerkung, dass man nicht ohne Weiteres aus den vorliegenden Daten auf die allgemeine Form schließen kann. Die "Endlichkeits-Annahme" ist genauso willkürlich wie die pragmatische Annahme, dass die angeführten Zahlen nur Teil einer längeren unendlichen Folge sind. Dass solche pragmatische Annahmen alles andere als unberechtigt, bis zu einem gewissen Grad sogar notwendig, weil allererst kommunikationsermöglichend, sind, zeigt Wittgenstein z.B. in dem von dir unten geposteten Tabellenbeispiel oder auch in dem Mosesbeispiel. Ich habe ja übrigens nicht nur die Unendlichkeit der dahinterliegenden Folge angenommen, sondern auch vorausgesetzt, dass es sich bei unseren Notationen um die gewöhnlichen mathematischen Notationen handelt, und nicht irgendeine formelhafte Fantasiesprache gemeint ist, etc.
- Ich habe die unten angeführten Wittgenstein Auszüge jetzt gelesen (zugegebenermaßen nicht so gründlich, wie es eine letzte Beurteilung erfordern würde, aber das ufert sonst aus), aber ich bin mir nicht sicher, ob Wittgenstein wirklich von den bloß in ihrer Auswertung verschiedenen Notationen spricht, auf die du so nachdrücklich aufmerksam machst. Die Beispiele, die er da bringt, sind ja vielmehr solcherart, dass der Schüler eine Zahlenreihe gezeigt bekommt, aber eine andere Form darin sieht, wie sich dann erst nach so und so vielen Folgengliedern zeigt. Es offenbart sich also wieder die Schwierigkeit des Erkennens (und hier auch: des Erklärens) einer allgemeinen (unendlichen) Regel auf Grundlage einer endlichen Anzahl von Beispielen – worauf ich in meinem allerersten Post bereits hingewiesen habe.--Realgeizt 20:56, 18. Dez. 2010 (UTC)
- Zusammenfassend: Wenn man sich auf "2,4,6,8,10,12,14,16" als Zeichenkette beschränkt, dann wird die Terminologie einfacher und das Problem der Verallgemeinerung verschwindet. Was aber als philosophisches Problem interessant bleibt ist, dass 2n+2 und n+2 wirklich zwei verschiedene Darstellungen sind in dem Sinn, dass es verschiedene Tätigkeit sind, 2n+2 geschlossen und n+2 rekursiv zu evaluieren. --PW 12:26, 17. Dez. 2010 (UTC)
- Wie ich die Folge jetzt evaluiere halte ich wirklich für nebensächlich. Ich kann ja dann auch hergehen und sagen okay, ich evaluiere jede dieser 2 Schreibweisen einmal mit Bleistift und einmal mit Kugelschreiber und einmal mit dem Computer. Das klingt jetzt vielleicht blöd, aber das soll nur illustrieren, dass wir uns damit schon auf einer ganz anderen Ebene befinden. Und ja, auch hier gibt es wieder interessante Aspekte, na klar. (Man denke etwa an Nietzsche und seine Schreibmaschine, und sein Zugeständnis: "Sie haben recht – unser Schreibzeug arbeitet mit an unseren Gedanken.") Aber ich denke hierauf sollte aus platonischer Sicht nicht das Augenmerk gelegt werden, sondern auf die gleichbleibende Form, die allen äußeren Darstellungen zu Grunde liegt. --Realgeizt 14:13, 17. Dez. 2010 (UTC)
- der Punkt ist, dass nicht die Folge evaluiert wird, sondern ein Ausdruck wie n+2 oder 2n+2. Und da macht es einen großen Unterschied, welche Regeln man dabei verwendet. Siehe oben. --PW 18:17, 17. Dez. 2010 (UTC)
- Wie ich die Folge jetzt evaluiere halte ich wirklich für nebensächlich. Ich kann ja dann auch hergehen und sagen okay, ich evaluiere jede dieser 2 Schreibweisen einmal mit Bleistift und einmal mit Kugelschreiber und einmal mit dem Computer. Das klingt jetzt vielleicht blöd, aber das soll nur illustrieren, dass wir uns damit schon auf einer ganz anderen Ebene befinden. Und ja, auch hier gibt es wieder interessante Aspekte, na klar. (Man denke etwa an Nietzsche und seine Schreibmaschine, und sein Zugeständnis: "Sie haben recht – unser Schreibzeug arbeitet mit an unseren Gedanken.") Aber ich denke hierauf sollte aus platonischer Sicht nicht das Augenmerk gelegt werden, sondern auf die gleichbleibende Form, die allen äußeren Darstellungen zu Grunde liegt. --Realgeizt 14:13, 17. Dez. 2010 (UTC)
- Zusammenfassend: Wenn man sich auf "2,4,6,8,10,12,14,16" als Zeichenkette beschränkt, dann wird die Terminologie einfacher und das Problem der Verallgemeinerung verschwindet. Was aber als philosophisches Problem interessant bleibt ist, dass 2n+2 und n+2 wirklich zwei verschiedene Darstellungen sind in dem Sinn, dass es verschiedene Tätigkeit sind, 2n+2 geschlossen und n+2 rekursiv zu evaluieren. --PW 12:26, 17. Dez. 2010 (UTC)
- "Form der Darstellung" und "Form". Das ist ein schönes Beispiel für eine Problemstellung, in der sich die Plausibilität platonisierender Gedanken zeigen lässt. Wir haben - wie soll man das sagen - eine Vorstellung, eine Idee, einen Begriff von "geraden Zahlen" und gehen davon aus, dass man diese Vorgabe auch notieren kann. Aber damit sind wir im Bereich der Materialität. Unversehens müssen wir zwischen verschiedenen Formen der Darstellung der Form unterscheiden. Und zwar präzise deshalb, weil sonst etwas auseinanderfallen würde, was wir nicht auseinanderfallen lassen wollen. Wenn ich eine Prüfungsfrage stelle ("Was ist ein feature freeze?)" will ich nicht eine einzige wortidentische "Antwort", sondern einen Ausdruck, der den Sinn "wiedergibt".
- "Verallgemeinerungen aufgrund begrenzter Daten". Das ist ein weit verbreiteter Zweck der Verallgemeinerung und daraus ergibt sich präzise das Formproblem. Wittgenstein diskutiert das unter dem Titel "Regelfolgen". S. Kripke hat ein schönes Buch darüber geschrieben. --anna 06:58, 17. Dez. 2010 (UTC)
aus den PU
kopiert von | hier. Hinweise auf bessere Quellen sind sehr willkommen. Hervorhebungen sind von mir. --PW 19:33, 17. Dez. 2010 (UTC)
84-87
Zum oben von mir angesprochenen Problem, dass auch präziserer Notation zu Missverständnissen führen kann.
84. Ich sagte von der Anwendung eines Wortes: sie sei nicht überall von Regeln begrenzt. Aber wie schaut denn ein Spiel aus, das überall von Regeln begrenzt ist? dessen Regeln keinen Zweifel eindringen lassen; ihm alle Löcher verstopfen. - Können wir uns nicht eine Regel denken, die die Anwendung der Regel regelt? Und einen Zweifel, den jene Regel behebt - und so fort? Aber das sagt nicht, daß wir zweifeln, weil wir uns einen Zweifel denken können. Ich kann mir sehr wohl denken, daß jemand jedesmal vor dem Offnen seiner Haustür zweifelt, ob sich hinter ihr nicht ein Abgrund aufgetan hat, und daß er sich darüber vergewissert, eh' er durch die Tür tritt (und es kann sich einmal erweisen, daß er recht hatte) - aber deswegen zweifle ich im gleichen Falle doch nicht.
85. Eine Regel steht da, wie ein Wegweiser. - Läßt er keinen Zweifel offen über den Weg, den ich zu gehen habe? Zeigt er, in welche Richtung ich gehen soll, wenn ich an ihm vorbei bin; ob der Straße nach, oder dem Feldweg, oder querfeldein? Aber wo steht, in welchem Sinne ich ihm zu folgen habe; ob in der Richtung der Hand, oder (z.B.) in der entgegengesetzten? - Und wenn statt eines Wegweisers eine geschlossene Kette von Wegweisern stünde, oder Kreidestriche auf dem Boden liefen, - gibt es für sie nur eine Deutung? - Also kann ich sagen, der Wegweiser läßt doch keinen Zweifel offen. Oder vielmehr: er läßt manchmal einen Zweifel offen, manchmal nicht. Und dies ist nun kein philosophischer Satz mehr, sondern ein Erfahrungssatz.
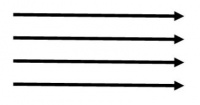
86. Ein Sprachspiel wie (2) werde mit Hilfe einer Tabelle gespielt. Die Zeichen, die A dem B gibt, seien nun Schriftzeichen. B hat eine Tabelle; in der ersten Spalte stehen die Schriftzeichen, die im Spiel gebraucht werden, in der zweiten, Bilder von Bausteinformen. A zeigt dem B ein solches Schriftzeichen; B sucht es in der Tabelle auf, blickt auf das gegenüberliegende Bild, etc. Die Tabelle ist also eine Regel, nach der er sich beim Ausführen der Befehle richtet. - Das Aufsuchen des Bildes in der Tabelle lernt man durch Abrichtung, und ein Teil dieser Abrichtung besteht etwa darin, daß der Schüler lernt, in der Tabelle mit dem Finger horizontal von links nach rechts zu fahren; also lernt, sozusagen eine Reihe horizontaler Striche zu ziehen. Denk dir, es würden nun verschiedene Arten eingeführt eine Tabelle zu lesen; nämlich einmal, wie oben, nach dem Schema:
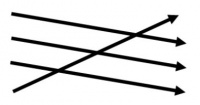
ein andermal nach diesem Schema:
oder einem andern, - So ein Schema werde der Tabelle beigefügt als Regel, wie sie zu gebrauchen sei. Können wir uns nun nicht weitere Regeln zur Erklärung dieser vorstellen? und war anderseits jene erste Tabelle unvollständig ohne das Schema der Pfeile? Und sind es die andern Tabellen ohne ihr Schema?
87. Nimm an, ich erkläre: »Unter ›Moses‹ verstehe ich den Mann, wenn es einen solchen gegeben hat, der die Israeliten aus Agypten geführt hat, wie immer er damals geheißen hat und was immer er sonst getan, oder nicht getan haben mag«. - Aber über die Wörter dieser Erklärung sind ähnliche Zweifel möglich wie die über den Namen »Moses« (was nennst du »Agypten«, wen »die Israeliten«, etc.?). Ja, diese Fragen kommen auch nicht zu einem Ende, wenn wir bei Wörtern wie »rot«, »dunkel«, »süß«, angelangt wären. - »Aber wie hilft mir dann eine Erklärung zum Verständnis, wenn sie doch nicht die letzte ist? Die Erklärung ist dann ja nie beendet; ich verstehe also noch immer nicht, und nie, was er meint!« - Als hinge eine Erklärung, gleichsam, in der Luft, wenn nicht eine andere sie stütze. Während eine Erklärung zwar auf einer andern, die man gegeben hat, ruhen kann, aber keine einer anderen bedarf - es sei denn, daß wir sie benötigen, um ein Mißverständnis zu vermeiden. Man könnte sagen: Eine Erklärung dient dazu, ein Mißverständnis zu beseitigen, oder zu verhüten - also eines, das ohne die Erklärung eintreten würde; aber nicht: jedes, welches ich mir vorstellen kann. Es kann leicht so scheinen, als zeigte jeder Zweifel nur eine vorhandene Lücke im Fundament; so daß ein sicheres Verständnis nur dann möglich ist, wenn wir zuerst an allem zweifeln, woran gezweifelt werden kann, und dann alle diese Zweifel beheben. Der Wegweiser ist in Ordnung, - wenn er, unter normalen Verhältnissen, seinen Zweck erfüllt.
143-146
Hier wird eine Situation des Zahlenreihen-schreiben-lernens beschrieben. Am Ende wird das oben für "Wegweiser" und "Erklärungen" gesagte auf algebraische Ausdrücke spezifiziert (siehe meine Hervorhebung).
143. Betrachten wir nun diese Art von Sprachspiel: B soll auf den Befehl des A Reihen von Zeichen niederschreiben nach einem bestimmten Bildungsgesetz. Die erste dieser Reihen soll die sein der natürlichen Zahlen im Dezimalsystem. - Wie lernt er dieses System verstehen? - Zunächst werden ihm Zahlenreihen vorgeschrieben und er wird angehalten, sie nachzuschreiben. (Stoß dich nicht an dem Wort »Zahlenreihen«, es ist hier nicht unrichtig verwendet!) Und schon hier gibt es eine normale und eine abnormale Reaktion des Lernenden. - Wir führen ihm etwa zuerst beim Nachschreiben der Reihe 0 bis 9 die Hand; dann aber wird die Möglichkeit der Verständigung daran hängen, daß er nun selbständig weiterschreibt. - Und hier können wir uns, z.B., denken, daß er nun zwar selbständig Ziffern kopiert, aber nicht nach der Reihe, sondern regellos einmal die, einmal die. Und dann hört da die Verständigung auf. - Oder aber er macht ›Fehler‹ in der Reihenfolge. - Der Unterschied zwischen diesem und dem ersten Fall ist natürlich einer der Häufigkeit. - Oder: er macht einen systematischen Fehler, er schreibt z.B. immer nur jede zweite Zahl nach; oder er kopiert die Reihe 0, 1, 2, 3, 4, 5, .... so: 1, 0, 3, 2, 5, 4, .... Hier werden wir beinahe versucht sein zu sagen, er habe uns falsch verstanden. Aber merke: Es gibt keine scharfe Grenze zwischen einem regellosen und einem systematischen Fehler. D.h., zwischen dem, was du einen »regellosen«, und dem, was du einen »systematischen Fehler« zu nennen geneigt bist. Man kann ihm nun vielleicht den systematischen Fehler abgewöhnen (wie eine Unart). Oder, man läßt seine Art des Kopierens gelten und trachtet, ihm die normale Art als eine Abart, Variation, der seinigen beizubringen. - Und auch hier kann die Lernfähigkeit unseres Schülers abbrechen.
144. Was meine ich denn, wenn ich sage »hier kann die Lernfähigkeit des Schülers abbrechen«? Teile ich das aus meiner Erfahrung mit? Natürlich nicht. (Auch wenn ich so eine Erfahrung gemacht hätte.) Und was tue ich denn mit jenem Satz? Ich möchte doch, daß du sagst: »Ja, es ist wahr, das könnte man sich auch denken, das könnte auch geschehen!« - Aber wollte ich Einen darauf aufmerksam machen, daß er imstande ist, sich dies vorzustellen? - Ich wollte dies Bild vor seine Augen stellen, und seine Anerkennung dieses Bildes besteht darin, daß er nun geneigt ist, einen gegebenen Fall anders zu betrachten: nämlich ihn mit dieser Bilderreihe zu vergleichen. Ich habe seine Anschauungsweise geandert. (Indische Mathematiker: »Sieh dies an!«)
145. Der Schüler schreibe nun die Reihe 0 bis 9 zu unsrer Zufriedenheit. - Und dies wird nur der Fall sein, wenn ihm dies oft gelingt, nicht, wenn er es einmal unter hundert Versuchen richtig macht. Ich führe ihn nun weiter in der Reihe und lenke seine Aufmerksamkeit auf die Wiederkehr der ersten Reihe in den Einern; dann auf diese Wiederkehr in den Zehnern. (Was nur heißt, daß ich gewisse Betonungen anwende, Zeichen unterstreiche, in der und der Weise untereinander schreibe, und dergleichen.) - Und nun setzt er einmal die Reihe selbständig fort, - oder er tut es nicht. - Aber warum sagst du das; das ist selbstverständlich! - Freilich; ich wollte nur sagen: die Wirkung jeder weiteren Erklärung hänge von seiner Reaktion ab. Aber nehmen wir nun an, er setzt, nach einigen Bemühungen des Lehrers, die Reihe richtig fort, d. h. so, wie wir es tun. Nun können wir also sagen: er beherrscht das System. - Aber wie weit muß er die Reihe richtig fortsetzen, damit wir das mit Recht sagen können? Es ist klar: du kannst hier keine Begrenzung angeben.
146. Wenn ich nun frage: »Hat er das System verstanden, wenn er die Reihe hundert Stellen weit fortsetzt?« Oder - wenn ich in unserm primitiven Sprachspiel nicht von ›verstehen‹ reden soll: Hat er das System inne, wenn er die Reihe bis dorthin richtig fortsetzt? - Da wirst du vielleicht sagen: Das System innehaben (oder auch: verstehen) kann nicht darin bestehen, daß man die Reihe bis zu dieser, oder bis zu jener Zahl fortsetzt; das ist nur die Anwendung des Verstehens. Das Verstehen selbst ist ein Zustand, woraus die richtige Verwendung entspringt. Und an was denkt man da eigentlich? Denkt man nicht an das Ableiten einer Reihe aus ihrem algebraischen Ausdruck? Oder doch an etwas Analoges? - Aber da waren wir ja schon einmal. Wir können uns ja eben mehr als eine Anwendung eines algebraischen Ausdrucks denken; und jede Anwendungsart kann zwar wieder algebraisch niedergelegt werden, aber dies führt uns selbstverständlich nicht weiter. - Die Anwendung bleibt ein Kriterium des Verständnisses.
151-152
Hier geht es um das "Erkennen" einer Folge, wie in unserer Ausgangssituation oben. Allerdings gibt es den kleinen Unterschied, dass A kontinuierlich die Angabe verlängert. Es wird damit suggeriert, dass A wirklich eine "unendliche" Folge meint. Meine obige Argumentation nützt dagegen den Umstand aus, dass "2,4,6,8,10,12,14,16" nicht als Anfang einer unendlichen Folge interpretiert werden muss. Wittgenstein beschreibt hier verschiedene Arten, "die Folge zu erkennen". Seine Formel n^2 + n + 1 entspricht unserem geschlossenen Ausdruck 2n+2. Für die "Reihe der Differenzen" eine Formel zu finden bedeutet dasselbe wie eine Rekursionsformel zu finden, d.h. das entspricht unserem n+2. Darüber hinaus ist es denkbar, dass man die Zahlenreihe einfach kennt.
151. Nun gibt es aber auch diese Verwendung des Wortes »wissen«: wir sagen »Jetzt weiß ich's!« - und ebenso »Jetzt kann ich's!« und »Jetzt versteh ich's!« Stellen wir uns dieses Beispiel vor: A schreibt Reihen von Zahlen an; B sieht ihm zu und trachtet, in der Zahlenfolge ein Gesetz zu finden. Ist es ihm gelungen, so ruft er: »Jetzt kann ich fortsetzen!« - Diese Fähigkeit, dieses Verstehen ist also etwas, was in einem Augenblick eintritt. Schauen wir also nach: Was ist es, was hier eintritt? - A habe die Zahlen 1, 5, 11, 19, 29 hingeschrieben; da sagt B, jetzt wisse er weiter. Was geschah da? Es konnte verschiedenerlei geschehen sein ; z.B.: Während A langsam eine Zahl nach der andern hinsetzte, ist B damit beschäftigt, verschiedene algebraische Formeln an den angeschriebenen Zahlen zu versuchen. Als A die Zahl 19 geschrieben hatte, versuchte B die Formel an = n^2 + n - 1; die nächste Zahl bestätigte seine Annahme. Oder aber: B denkt nicht an Formeln. Er sieht mit einem gewissen Gefühl der Spannung zu, wie A seine Zahlen hinschreibt; dabei schwimmen ihm allerlei unklare Gedanken im Kopf. Endlich fragt er sich »Was ist die Reihe der Differenzen?« Er findet: 4, 6, 8, 10 und sagt: Jetzt kann ich weiter. Oder er sieht hin und sagt: »Ja, die Reihe kenn' ich« - und setzt sie fort; wie er's etwa auch getan hätte, wenn A die Reihe 1, 3, 5, 7, 9 hingeschrieben hätte. - Oder er sagt garnichts und schreibt bloß die Reihe weiter. Vielleicht hatte er eine Empfindung, die man »das ist leicht!« nennen kann. (Eine solche Empfindung ist z.B. die eines leichten, schnellen Einziehens des Atems, ähnlich wie bei einem gelinden Schreck.)
152. Aber sind denn diese Vorgänge, die ich da beschrieben habe, das Verstehen? »B versteht das System der Reihe« heißt doch nicht einfach: B fällt die Formel »an = ....« ein! Denn es ist sehr wohl denkbar, daß ihm die Formel einfällt und er doch nicht versteht. »Er versteht« muß mehr beinhalten als: ihm fällt die Formel ein. Und ebenso auch mehr, als irgendeiner jener, mehr oder weniger charakteristischen, Begleitvorgänge, oder Äußerungen, des Verstehens. (Das Ab- und Zunehmen einer Schmerzempfindung, das Hören einer Melodie, eines Satzes: seelische Vorgänge.)
185-190
Diesen Teil musste ich einfach hier herein kopieren, weil es um Beispiele der obigen Form (Tabelle) geht. Zu beachten ist aber wieder, dass es um die potentiell unendlich lange Folgen geht, nicht wie oben um endliche Zeichenketten. Noch einmal wird aber darauf insistiert, dass der Grund für unsere relative Sicherheit beim Übersetzen des algebraischen Ausdrucks daher rührt, dass wir es so gelernt haben und so gewöhnt sind.
185. Gehen wir nun zu unserm Beispiel (143) zurück. Der Schüler beherrscht jetzt - nach den gewöhnlichen Kriterien beurteilt - die Grundzahlenreihe. Wir lehren ihn, nun auch andere Reihen von Kardinalzahlen anschreiben und bringen ihn dahin, daß er z.B. auf Befehle von der Form »+n« Reihen der Form 0, n, 2n, 3n,
etc. anschreibt; auf den Befehl »+1« also die Grundzahlenreihe. - Wir hätten unsre Übungen und Stichproben seines Verständnisses im Zahlenraum bis 1000 gemacht. Wir lassen nun den Schüler einmal eine Reihe (etwa »+2«) über 1000 hinaus fortsetzen, - da schreibt er: 1000, 1004, 1008, 1012. Wir sagen ihm: »Schau, was du machst!« - Er versteht uns nicht. Wir sagen: »Du solltest doch zwei addieren; schau, wie du die Reihe begonnen hast!« - Er antwortet: »Ja! Ist es denn nicht richtig? Ich dachte, so soll ich's machen.« - Oder nimm an, er sagte, auf die Reihe weisend: »Ich bin doch auf die gleiche Weise fortgefahren!« - Es würde uns nun nichts nützen, zu sagen »Aber siehst du denn nicht....?« - und ihm die alten Erklärungen und Beispiele zu wiederholen. - Wir könnten in so einem Falle etwa sagen: Dieser Mensch versteht von Natur aus jenen Befehl, auf unsre Erklärungen hin, so, wie wir den Befehl: »Addiere bis 1000 immer 2, bis 2000 4, bis 3000 6, etc.«. Dieser Fall hätte Ähnlichkeit mit dem, als reagierte ein Mensch auf eine zeigende Gebärde der Hand von Natur damit, daß er in der Richtung von der Fingerspitze zur Handwurzel blickt, statt in der Richtung zur Fingerspitze.
186. »Was du sagst, läuft also darauf hinaus, es sei zum richtigen Befolgen des Befehls ›+n‹ auf jeder Stufe eine neue Einsicht - Intuition - nötig.« - Zur richtigen Befolgung! Wie wird denn entschieden, welches an einem bestimmten Punkt der richtige Schritt ist? - »Der richtige Schritt ist der, welcher mit dem Befehl - wie er gemeint war - übereinsstimmt.« - Du hast also zur Zeit, als du den Befehl »+2« gabst, gemeint, er solle auf 1000 1002 schreiben - und hast du damals auch gemeint, er solle auf 1866 1868 schreiben, und auf 100034 100036, usf. - eine unendliche Anzahl solcher Sätze? - »Nein; ich habe gemeint, er solle nach jeder Zahl, die er schreibt, die zweitnächste schreiben; und daraus folgen ihres Orts alle jene Sätze.« - Aber es ist ja gerade die Frage, was, an irgendeinem Ort, aus jenem Satz folgt. Oder auch - was wir an irgendeinem Ort »Übereinstimmung« mit jenem Satz nennen sollen (und auch mit der Meinung, die du damals dem Satz gegeben hast, - worin immer diese bestanden haben mag). Richtiger, als zu sagen, es sei an jedem Punkt eine Intuition nötig, wäre beinah, zu sagen; es sei an jedem Punkt eine neue Entscheidung nötig.
187. »Ich habe aber doch auch damals, als ich den Befehl gab, schon gewußt, daß er auf 1000 1002 schreiben soll!« - Gewiß; und du kannst sogar sagen, du habest es damals gemeint; nur sollst du dich nicht von der Grammatik der Wörter »wissen« und »meinen« irreführen lassen. Denn du meinst ja nicht, daß du damals an den Übergang von 1000 auf 1002 gedacht hast - und wenn auch an diesen Übergang, so doch an andre nicht. Dein »Ich habe damals schon gewußt ....« heißt etwa: »Hätte man mich damals gefragt, welche Zahl er nach 1000 schreiben soll, so hätte ich geantwortet ›;1002‹.« Und daran zweifle ich nicht. Es ist das eine Annahme etwa von der Art dieser: »Wenn er damals ins Wasser gefallen wäre, so wäre ich ihm nachgesprungen.« - Worin lag nun das Irrige deiner Idee?
188. Da möchte ich zuerst sagen: Deine Idee sei die gewesen, jenes Meinen des Befehls habe auf seine Weise alle jene Übergänge doch schon gemacht: deine Seele fliege beim Meinen, gleichsam, voraus und mache alle Übergänge, ehe du körperlich bei dem oder jenem angelangt bist. Du warst also zu Ausdrücken geneigt, wie: »Die Übergänge sind eigentlich schon gemacht; auch ehe ich sie schriftlich, mündlich, oder in Gedanken mache.« Und es schien, als wären sie in einer einzigartigen Weise vorausbestimmt, antizipiert - wie nur das Meinen die Wirklichkeit antizipieren könne.
189. »Aber sind die Übergänge also durch die algebraische Formel nicht bestimmt?« - In der Frage liegt ein Fehler. Wir verwenden den Ausdruck: »die Übergänge sind durch die Formel .... bestimmt«. Wie wird er verwendet? - Wir können etwa davon reden, daß Menschen durch Erziehung (Abrichtung) dahin gebracht werden, die Formel y=x2 so zu verwenden, daß Alle, wenn sie die gleiche Zahl für x einsetzen, immer die gleiche Zahl für y herausrechnen. Oder wir können sagen: »Diese Menschen sind so abgerichtet, daß sie alle auf den Befehl ›+3‹ auf der gleichen Stufe den gleichen Übergang machen. Wir könnten dies so ausdrücken: Der Befehl ›+3‹ bestimmt für diese Menschen jeden Übergang von einer Zahl zur nächsten völlig.« (Im Gegensatz zu andern Menschen, die auf diesen Befehl nicht wissen, was sie zu tun haben; oder die zwar mit völliger Sicherheit, aber ein jeder in anderer Weise, auf ihn reagieren.) Wir können anderseits verschiedene Arten von Formeln, und zu ihnen gehörige verschiedene Arten der Verwendung (verschiedene Arten der Abrichtung) einander entgegensetzen. Wir nennen dann Formeln einer bestimmten Art (und der dazugehörigen Verwendungsweise) »Formeln, welche eine Zahl y für ein gegebenes x bestimmen«, und Formeln anderer Art solche, »die die Zahl y für ein gegebenes x nicht bestimmen«. (y=x2 wäre von der ersten Art, y≠x2 von der zweiten.) Der Satz »Die Formel .... bestimmt eine Zahl y« ist dann eine Aussage über die Form der Formel - und es ist nun zu unterscheiden ein Satz wie dieser: »Die Formel, die ich hingeschrieben habe, bestimmt y« oder »Hier steht eine Formel, die y bestimmt« - von einem Satz der Art: »Die Formel y=x2 bestimmt die Zahl y für ein gegebenes x«. Die Frage »Steht dort eine Formel, die y bestimmt?« heißt dann dasselbe wie: »Steht dort eine Formel dieser Art, oder jener Art?« - was wir aber mit der Frage anfangen sollen »Ist y=x2 eine Formel, die y für ein gegebenes x bestimmt?« ist nicht ohne weiteres klar. Diese Frage könnte man etwa an einen Schüler richten, um zu prüfen, ob er die Verwendung des Wortes »bestimmen« versteht; oder es könnte eine mathematische Aufgabe sein, in einem bestimmten System zu beweisen, daß x nur ein Quadrat besitzt.
190. Man kann nun sagen: »Wie die Formel gemeint wird, das bestimmt, welche Übergänge zu machen sind.« Was ist das Kriterium dafür, wie die Formel gemeint ist? Etwa die Art und Weise, wie wir sie ständig gebrauchen, wie uns gelehrt wurde, sie zu gebrauchen. Wir sagen z.B. Einem, der ein uns unbekanntes Zeichen gebraucht: »Wenn du mit ›x!2‹ meinst x2, so erhältst du diesen Wen für y, wenn du 2x damit meinst, jenen.« - Frage dich nun: Wie macht man es, mit »x!2« das eine, oder das andere meinen? So kann also das Meinen die Übergänge zum voraus bestimmen.